蚁群算法(Ant System)(AS)
基本蚁群算法(AS)是采用人工蚂蚁的行走路线来表示待求解问题可行解的一种方法。没只蚂蚁在解空间中独立地搜索可行解,当它们碰到一个没有走过的路口时,就随机挑选一条路径前行,同时释放出与路径程度有关的信息素。路径越短信息素的浓度就越大。当后续的人工蚂蚁再次碰到这个路口的时候,以相对较大的概率选择信息素较多的路径,并在“行走路线”上留下更多的信息素,影响后来的蚂蚁,形成正反馈机制 。随着算法的推进,代表最优解路线上的信息素越来越多,选择它的蚂蚁也逐渐增多,其他路径上的信息素却会随着时间的流逝而逐渐消减,最终整个蚁群在正反馈的作用下集中到代表最优解的线路上,也就找到了最优解。在整个寻优过程中,单只蚂蚁的选择能力有限,但蚁群具有高度的自组织性,通过信息素交换路径信息,形成集体自催化行为,找到最优路径。
基本蚁群算法的具体实现
基于蚁周模型进行实现: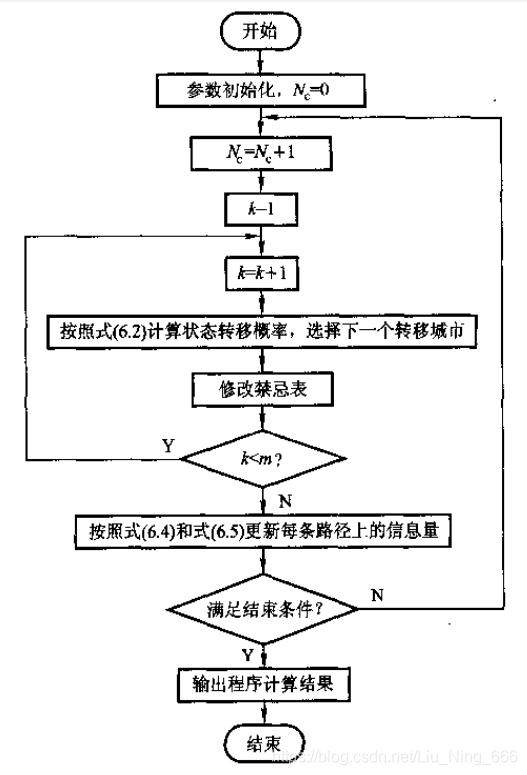


步骤
第1步:初始化参数。时间
t
t
t=0,循环次数
N
N
N
c
c
c,设置最大循环次数
N
N
N
c
m
a
x
cmax
cmax,令路径(
i
,
j
i,j
i,j)的初始化信息量
τ
\tau
τ
i
j
ij
ij(
t
t
t)
=
c
o
n
s
t
=const
=const,初始时刻
τ
\tau
τ
i
j
ij
ij(
0
0
0)
=
0
=0
=0。
第2步:将
m
m
m只蚂蚁随机放在
n
n
n个城市上。
第3步:循环次数
N
N
N
c
c
c=
N
N
N
c
c
c+1。
第4步:令蚂蚁禁忌表索引号
k
k
k=1。
第5步:
k
k
k =
k
+
1
k+1
k+1。
第6步:根据状态转移概率公式(6.2)计算蚂蚁选择城市
j
j
j的概率,
j
j
j
∈
\in
∈{
C
−
t
a
b
u
C-tabu
C−tabu
k
k
k}。
第7步:选择具有最大状态转移概率的城市,将蚂蚁移动到该城市,并把该城市记入禁忌表中。
第8步:若没有访问完集合
C
C
C中的所有城市,即
k
<
m
k<m
k<m,跳转至第5步;否则,转到第9步。
第9步:根据式(6.4)和(6.5)更新每条路径上的信息量。
第10步:若满足结束条件,循环结束输出计算结果;否则清空禁忌表并跳转到第3步。
改进的蚁群算法
主要两个改进目的:(1)在合理的时间内提高蚁群算法的寻优能力,改善其全局收敛性。(2)使蚁群算法能够应用于连续域问题。
自适应蚁群算法
即对蚁群算法的状态转移概率、信息挥发因子、信息量等因素采用自适应调节策略。典型的有两种:1、蚁群系统(Ant Colony System)(ACS)2、最大最小蚁群系统(MAX-MIN Ant System)(MMAS)
蚁群系统(Ant Colony System)(ACS)
ACS解决了基本蚁群算法在构造解过程汇总,随机选择策略造成的算法进化速度慢的缺点。该算法在每一次循环中仅让最短路径上的信息量作更新,且以较大的概率让信息量最大的路径被选中,充分利用学习机制,强化最优信息的反馈。ACS的核心思想是:蚂蚁在寻找最佳路径的过程中只能使用局部信息,即采用局部信息对路径上的信息量进行调整;在所有进行寻优的蚂蚁结束路径的搜索后,路径上的信息量会再一次调整,这次采用的是全局信息,而且只对过程中发现的最好路径上的信息量进行加强。
ACS模型与AS模型的主要区别有三点:(1)蚂蚁的状态转移规则不同(2)全局更新规则不同(3)新增了对各条路径信息量调整的局部更新规则
ACS伪代码如下



